[백준] 14285 간선 끊어가기
정점 n개, m개의 간선으로 이루어진 무방향 그래프가 주어진다. 그리고 그래프 내에 있는 m개의 가중치 간선의 정보가 있는 간선리스트가 주어진다. 간선리스트에 있는 간선 하나씩 그래프에 제거해 나갈 것이다. 이때, 특정 정점 s와 t가 비연결이 되는 시점에서 간선 제거를 멈출 것이다. s와 t가 비연결이 되는 시점의 지운 간선의 가중치의 합이 최대가 되게 제거하는 간선의 순서를 조정할 때, 그 최댓값을 구하시오. → 그래프에서 간선을 지울건데, 지운 간선의 총합이 최대이어야하고 간선을 지울때 s, t가 끊어진다면 그때 멈추어야함.
→ 그럼 비연결이 될 때까지 최대한 많은 간선을 지워야하고, 즉 s-t를 잇는 경로를 제외한 모든 간선들을 지우게 됨. 그리고 추가로 s-t를 잇는 최단 경로(간선의 합이 최소이면 나머지 지울 수 있는 경로(가중치)가 더 늘어나기 때문에 최단경로)에서 가장 큰 가중치를 갖는 간선을 지우면 그때 지운 간선의 합이 최대값이 됨.
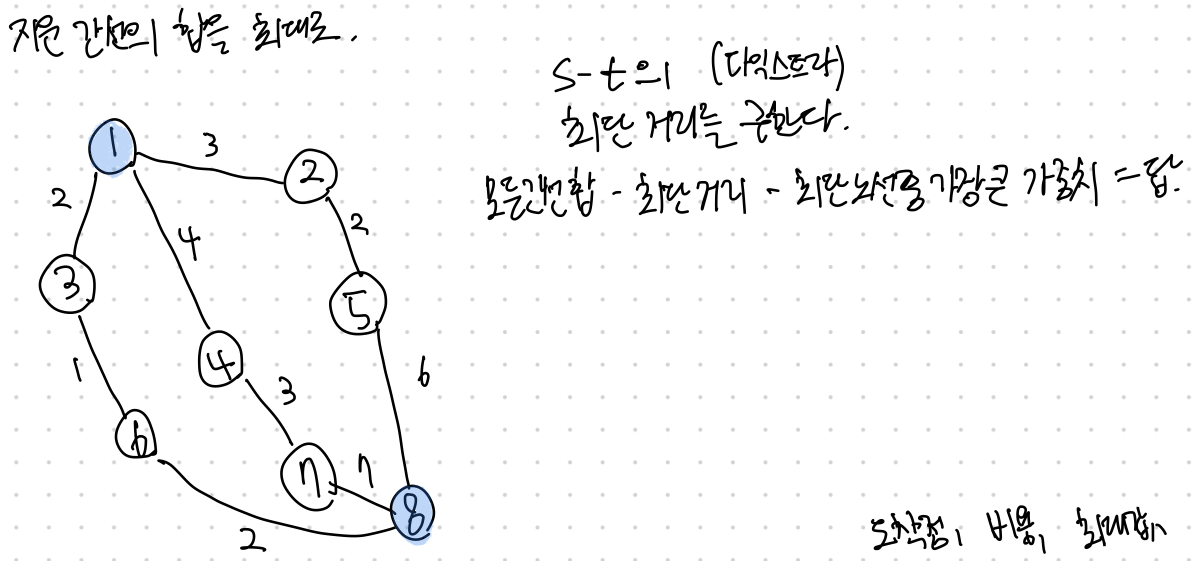
그래서 다익스트라를 구현하고, 모든 간선의 총합 - 최단거리 - 최단경로 중 가장 큰 가중치 를 계산해서 답을 내려고 했으나 간선 정보를 인접 리스트로 구현하여 최단 경로 안에서 가장 큰 가중치를 갖는 간선을 찾기에 비효율적이라고 생각함... + 생각 안남
그래서 최단경로에 거쳐온 간선 중 가장 큰 가중치 값을 포함하는 표현으로 바꿈.
dist[i] : 시작 노드에서 i 노드로 갈 때 가장 최단 경로, 근데 이제 거쳐온 간선 중 가장 큰 가중치 값은 뺀.
그럼 처음에 생각했던 답의 계산식인 (모든 간선의 총합 - 최단거리 - 최단경로 중 가장 큰 가중치) 에서 (모든 간선의 총합 - dist[i]) 로 바꿀 수 있게 됨.
다익스트라에서 최단 경로에 대해 계산할 때는 다음과 같음.
- 시작노드에서 a 노드까지 걸린 (최단 경로 - 그 경로 중 가장 큰 가중치 값(=a_max)) (=dist[a])
- dist[b] = 현재 최단 경로 - 경로 중 가장 큰 가중치 값.
1. 여기서 지금 b의 최단경로를 비교해 a를 거치는게 더 최단인지 확인하는 과정이 필요함. 지금 dist[b] = b까지의 최단 경로 - 그 경로 중 가장 최대값(=b_max)이 됨. (여기서 문제에서 찾는건 지운값이 최대가 되도록, 즉 사이를 잇는 간선의 합이 최소가 되어야함. dist는 경로 중 가장 큰 값을 뺀 값이므로, 문제에서 구하는 간선의 합 최소가 됨. 그래서 이 개념을 그대로 들고 비교해야함.💡)
2. 만약에 시작노드부터 b까지의 경로가 시작-...-a-b가 최단경로라면 다음 계산식이 됨. (시작노드에서 a 노드까지 걸린 최단경로 + ab 간선 + {그중max}).
3. 이를 현재 갖고 있는 dist로 표현하면 (dist[a] + a_max + ab 간선 + {그중max}) 가 된다. 즉, dist[b]는 시작노드에서 a를 거치고, a에서 b로 가는 경로 중 최대값을 뺀것이 됨.
4-1. 만약 a를 거쳐왔을 때의 가중치 최대값(=a_max)이 새로운 ab 간선보다 크다면, 경로 중 최대값은 그대로 a_max임. 따라서 dist[b] = dist[a] + ab간선
4-2. 만약 a를 거쳐왔을 때의 가중치 최대값(=a_max)이 새로운 ab 간선보다 작다면, 경로 중 최대값은 ab 간선이 된다. 따라서 dist[a]에 존재하는 a_max 값은 지워줘야 함. dist[b] = dist[a]+a_max(이전최대값제거) +ab간선(새로운간선추가) -ab간선(경로중최대값)

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
#define MAX_n 100001
#define INF 987654321
int n, m, a, b, c, s, t, sum = 0;
vector<pair<int, int>> edges[MAX_n];
int dist[MAX_n];
void dijk(int cur_node) {
priority_queue<pair<int, pair<int, int>>> que;
int cur_cost = 0, nxt_node, nxt_cost, cur_max, new_cost;
que.push({cur_cost, {cur_node, cur_cost}});
dist[cur_node] = cur_cost;
while (!que.empty()) {
pair<int, pair<int, int>> cur = que.top();
cur_node = cur.second.first;
cur_cost = -cur.first;
cur_max = cur.second.second;
que.pop();
if (dist[cur_node] < cur_cost) continue;
for (pair<int, int> nxt : edges[cur_node]) {
nxt_node = nxt.first;
nxt_cost = nxt.second;
// dist = 진짜 경로 - 경로 중 가장 큰 값
// 만약 지나온 간선(cur_max)보다 현재 엣지(nxt_cost)가 더 큰 값을 지닌다면 cur_cost + cur_max + nxt_cost - nxt_cost
// 작은값을 지닌다면 cur_cost + (cur_max - cur_max) + nxt_cost
new_cost = cur_cost + cur_max + nxt_cost - max(cur_max, nxt_cost);
if (dist[nxt_node] > new_cost) {
dist[nxt_node] = new_cost;
que.push({-new_cost, {nxt_node, max(cur_max, nxt_cost)}});
}
}
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> m;
for (int i = 0; i < m; ++i) {
cin >> a >> b >> c;
edges[a].push_back({b, c});
edges[b].push_back({a, c});
sum += c;
}
fill(&dist[0], &dist[0]+MAX_n, INF);
cin >> s >> t;
dijk(s);
cout << sum - dist[t];
return 0;
}
'* 언어 | 알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| [백준] 5012 불만 정렬 (0) | 2023.08.13 |
|---|---|
| [백준] 3006 터보소트 (0) | 2023.08.12 |
| [백준] 14574 헤븐스 키친 (0) | 2023.08.10 |
| [백준] 1365 꼬인 전깃줄 (0) | 2023.08.09 |
| [백준] 5419 북서풍 (0) | 2023.08.07 |












