[LG Aimers] Forecasting (1) 수요예측 기법 및 예측 오차
2023. 7. 22. 16:30
- 테마파크로 보는 수요예측(forecasting)의 중요성
- 몇 개의 놀이기구가 있어야할지, 각 놀이기구의 수용인원, 운행시간은 어떻게 해야할지. 놀이기구의 운영인원은 시간마다 몇 사람으로 배치할지.
- 테마파크의 음식점은 무엇이 있어야 하는지, 무슨 메뉴가 있어야 하는지.
- → 비즈니스의 가장 처음이 되는 부분. demand의 forecasting이 되어야 함. (수요예측).
- → 수요예측을 잘못하면 금전적 등의 많은 문제가 생김.
수요예측 기법
| 방법 | 특징 | 장단점 |
|---|---|---|
| Qualitative(정성적) | Subjective: 사람의 의견을 기반 | 전문가의 노하우가 담김. 하지만 경우에 따라 Over-estimate되거나 Under-estimate됨. |
| Quantitative(정량적) | Objective: numeric data, equation을 기반 | Consistency,일관적. 하지만 많은 데이터가 필요 |
- 주로 두 방법이 같이 사용됨. 정량적 방법과 전문가의 의견이 결합되도록.
Time Series Forecasts
- 가정 : 과거의 history가 미래를 예측하는데 도움이 될 것이다.
- Time series data를 사용.

- Fluctuates About A Constant Mean. 평균 수치에 대한 fluctuation(요동)을 갖는다.
- fluctuation과, 증가하는 현상을 갖는다.
- fluctuation과, 계절성을 갖는다.
- $A_t$ : period t에 대한 실제(Actual) 관측된 수요
- $F_{t+1}$ : period t+1에 대해 예측된(Forecast) 수요. (period t까지의 실제 수요를 가지고 예측, 만들어진)
1. Fluctuates About A Constant Mean

Example: Forecasting Demand for Polio Vaccines
Method 1: Naive Method
- 이전 달의 수요를 그대로 사용하는 것.

Method 2: Simple Average
- 이전 달들의 수요들을 모두 평균내어 사용하는 것.
- 하지만 모든 과거의 (예를 들어 10년 전) 데이터를 사용하는 것이 맞는 것인가? → Method3 Moving Average
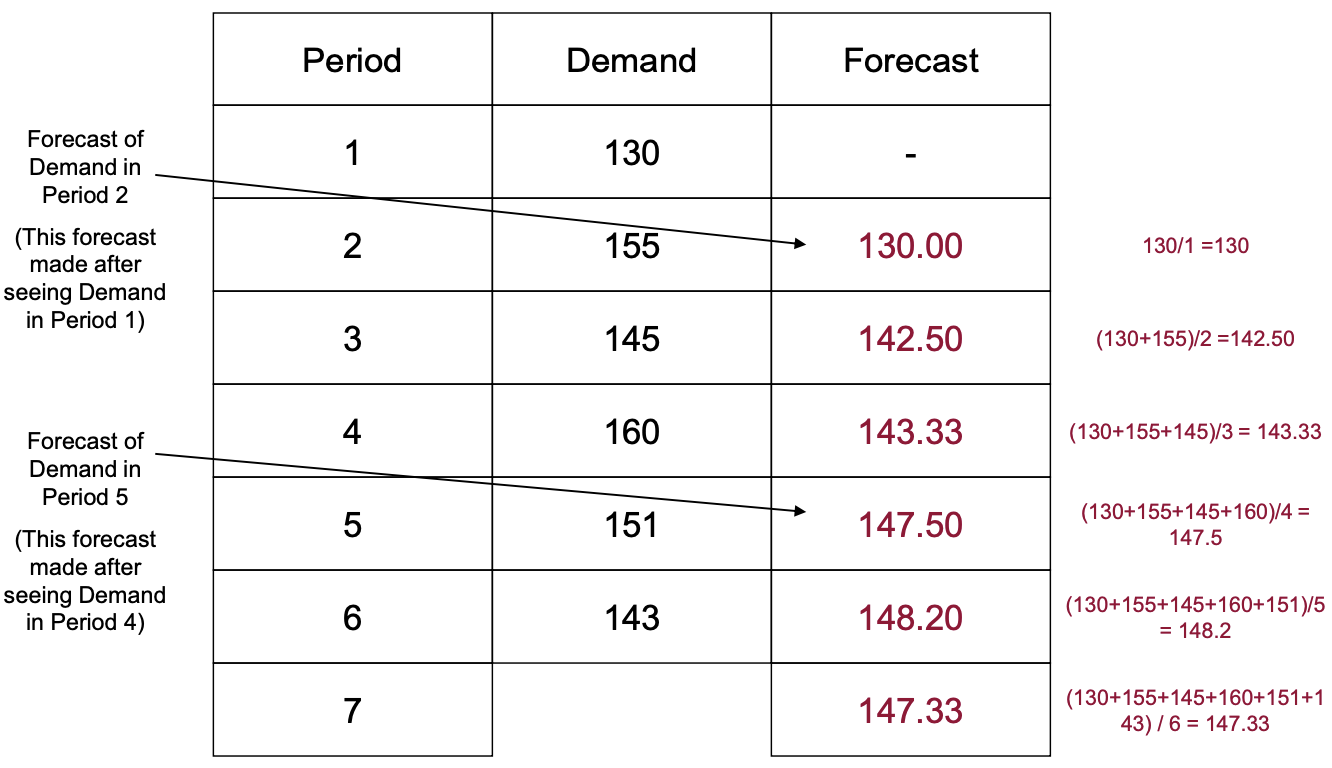
Method 3: Moving Average
- n개의 period 수요값만을 사용, 이동 평균을 사용하는 것.
- 사용하는 과거 값들을 모두 같은 가중치로 사용하는 것이 맞는 것인가? → Method4
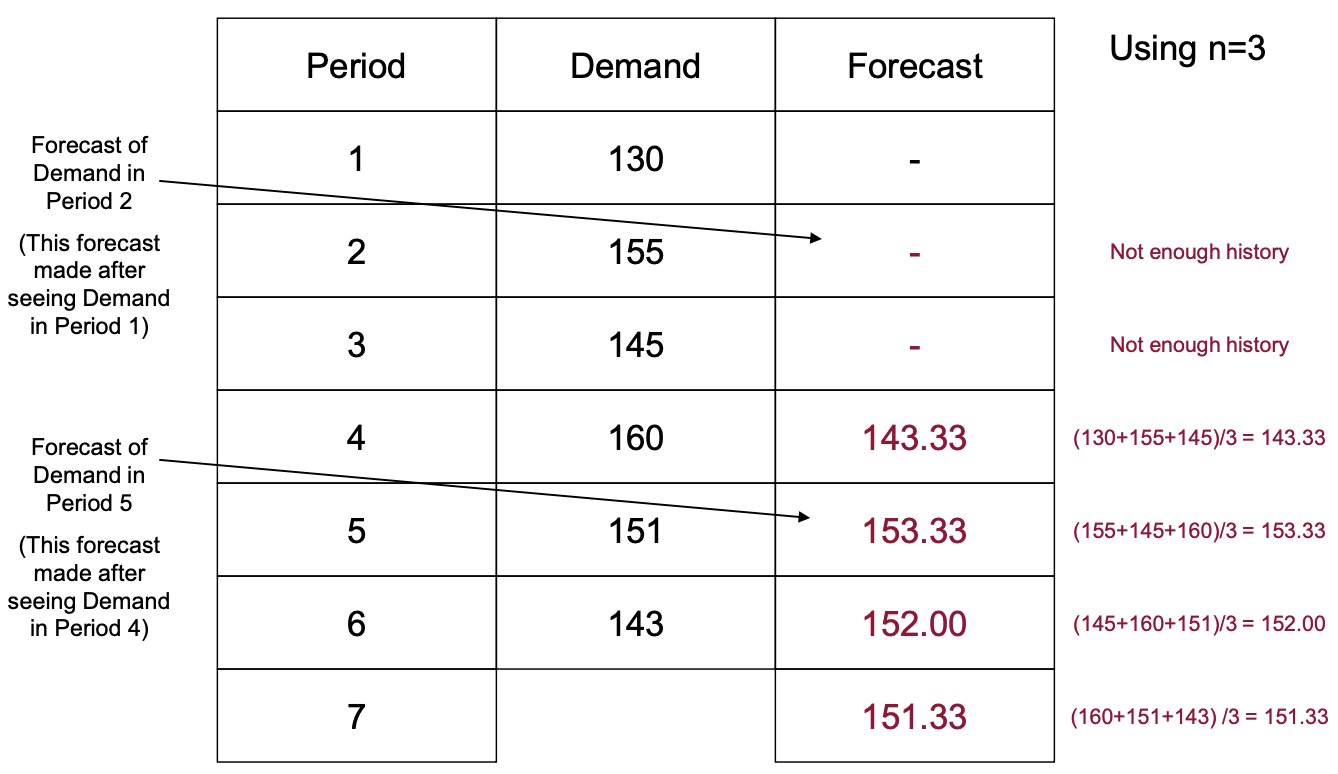
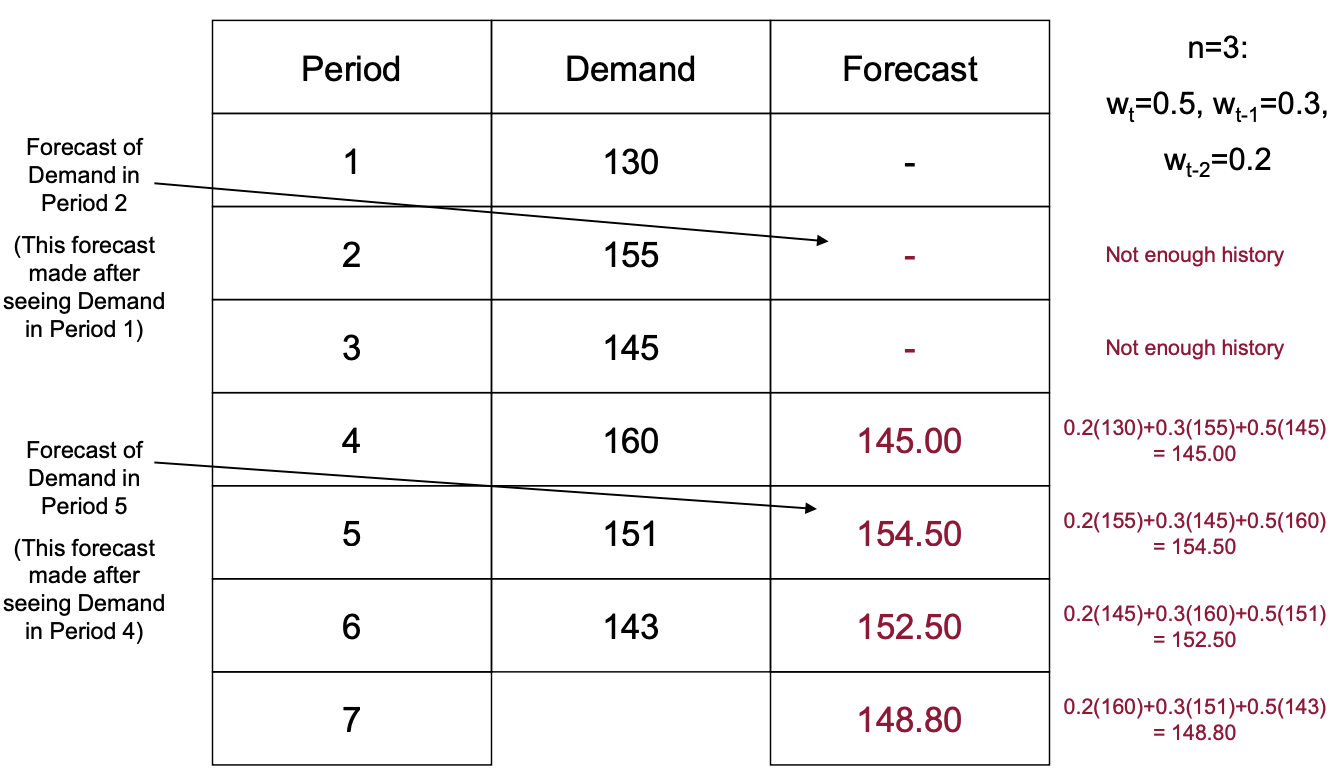
Method 4: Weighted Moving Average
- n개의 period 수요값만을 사용, 이동 평균을 사용하는 것.
- n개의 weight 값을 사용.
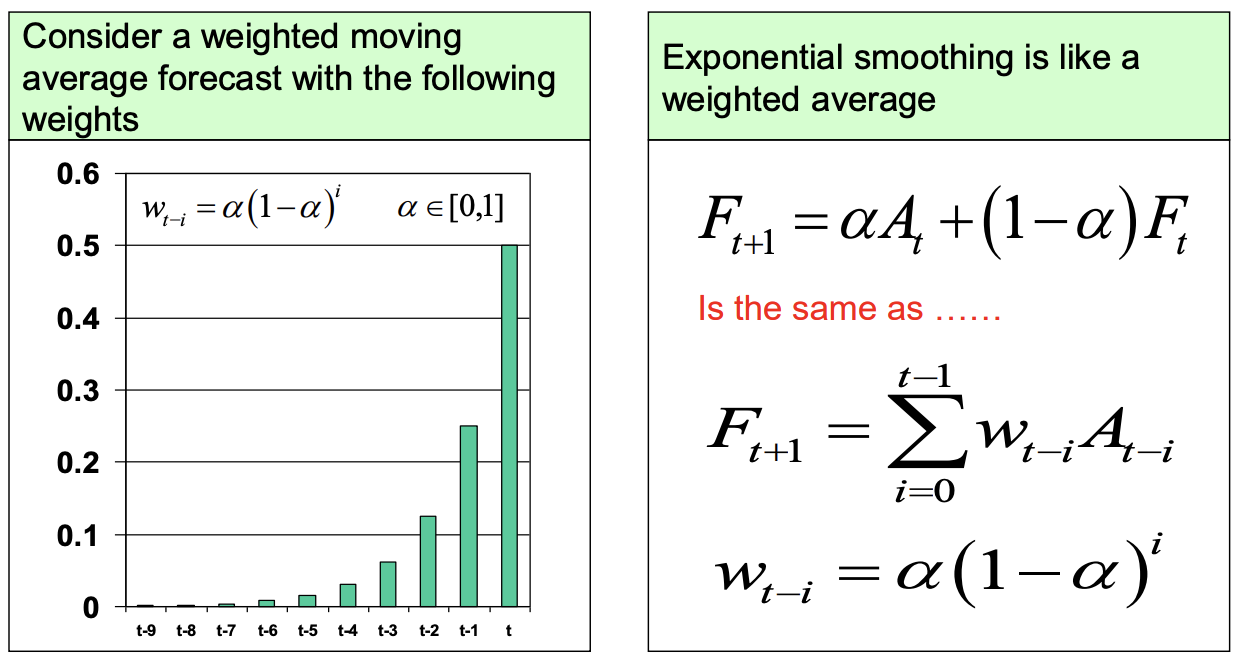
Method 5: Exponential Smoothing Forecast
- 이전 달들의 수요들을 모두 사용하는 것.
- 하지만 weight은 다르게 줌. (최근이 크도록 exponetial을 이용)
- smoothing factor $\alpha$ : 가장 최근것의 weight
- 가장 처음 예측을 위해, 처음 달의 Actual Demand를 그대로 사용하는 방법
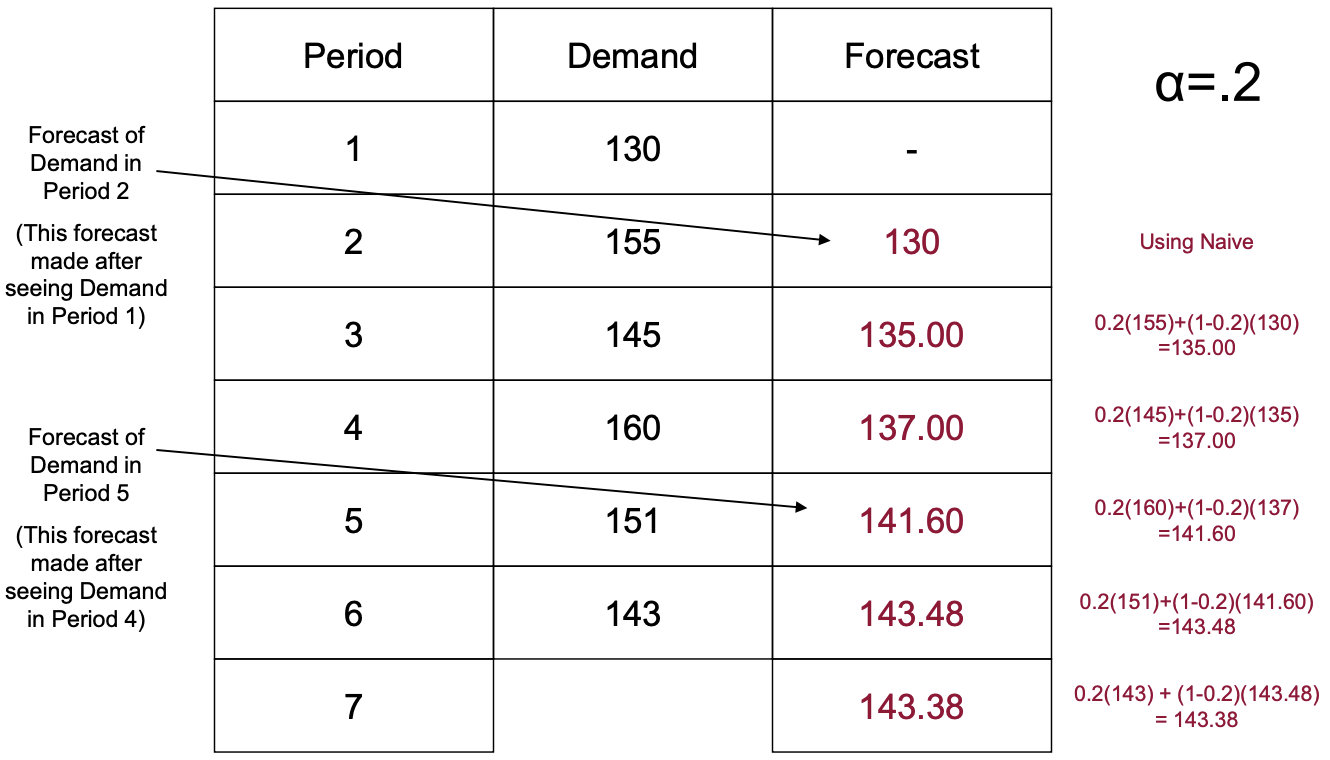
- 가장 처음 예측을 위해, 처음 달의 Forecast를 만들어서 사용하는 방법.
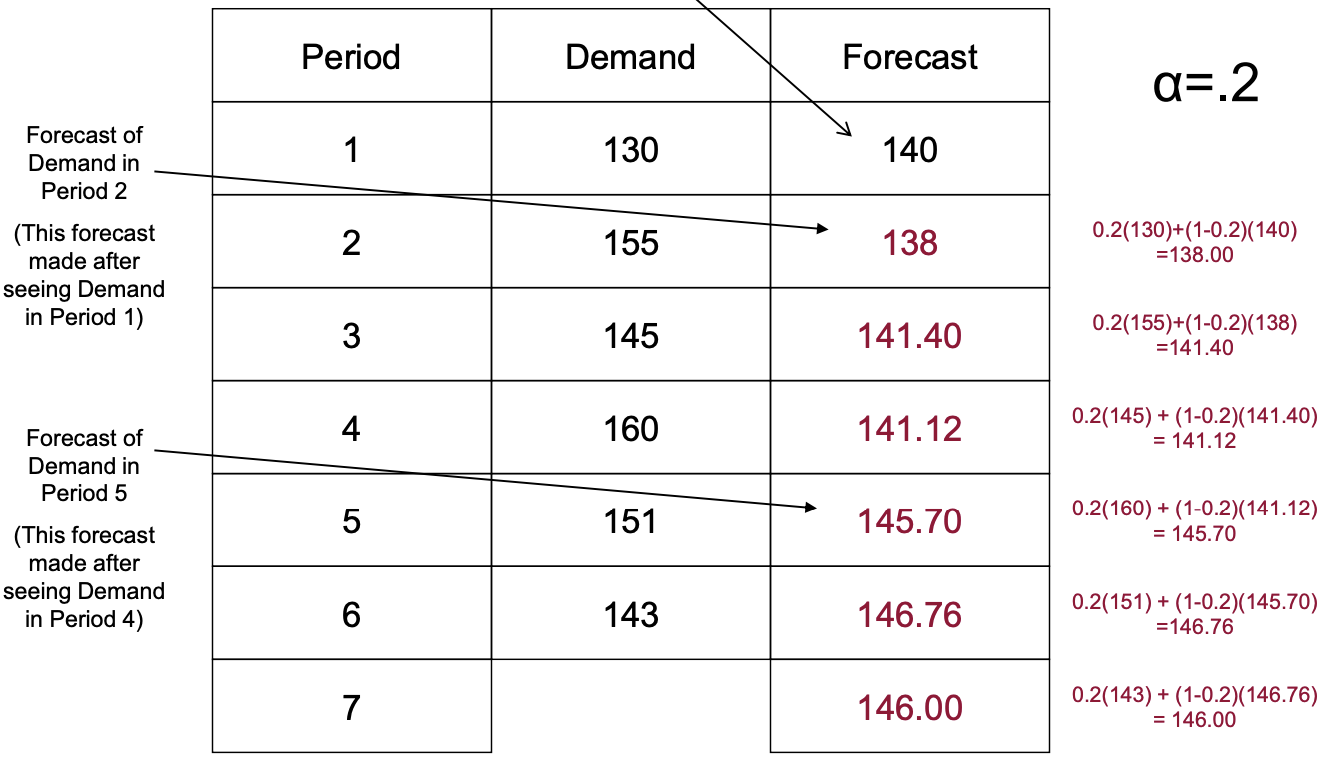
급격한 Demand의 변화가 일어날 때
Example1 :
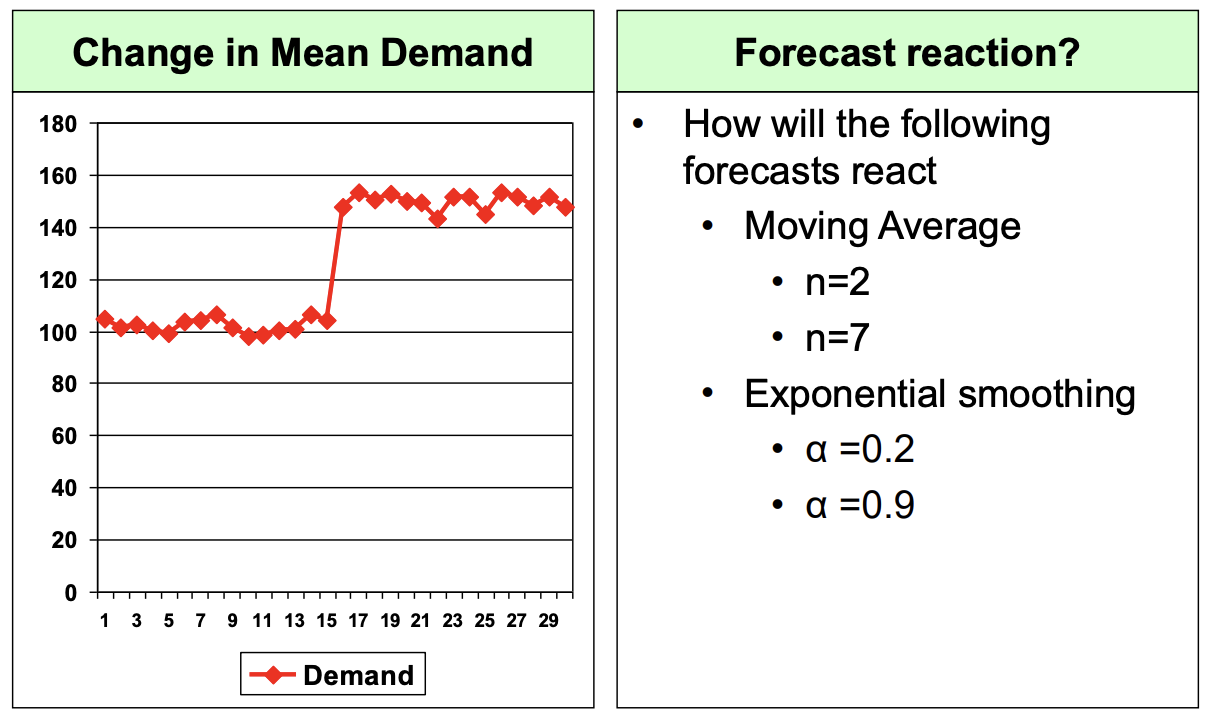
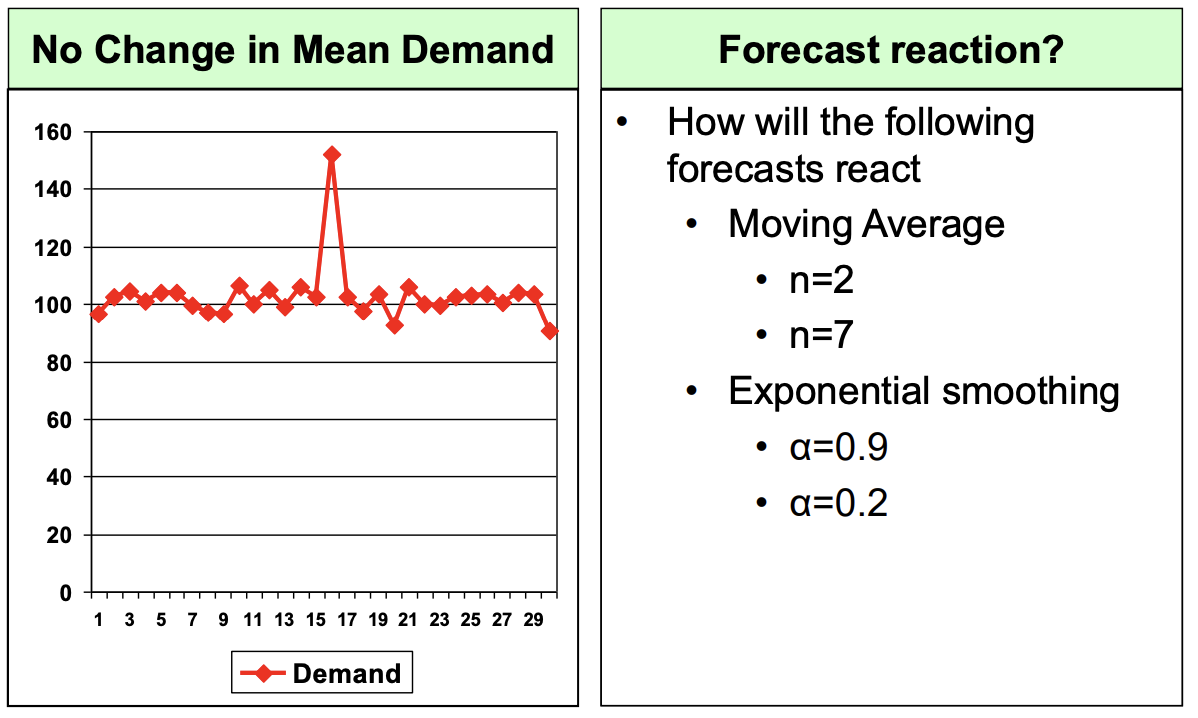
- 예기치못한 수요 증가, 감소가 일어난다면 (예시: 코로나로 인해 마스크 수요 급증) forecast가 어떻게 변화할까?
- Moving Average(method 3); n이 2, 7 일 때.
- Exponential Smoothing(method 5); $\alpha$가 0.9, 0.2 일 때. 각각 비교해보자.
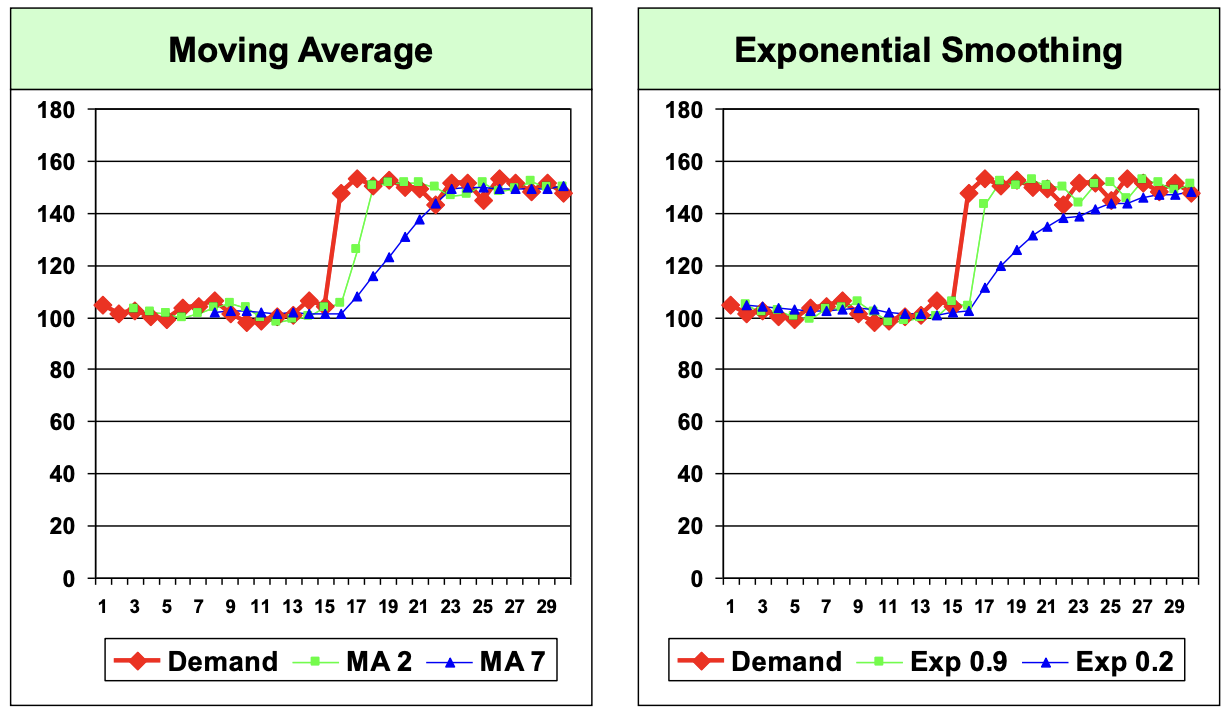
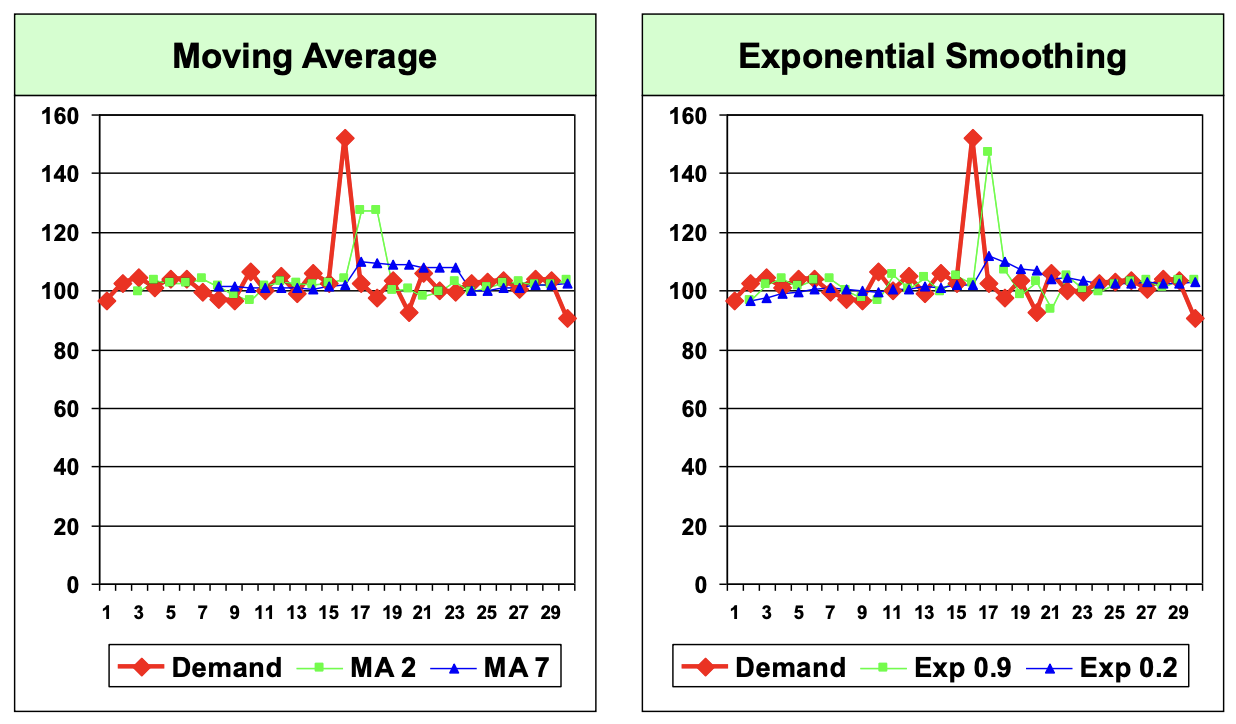
- Moving Average(method 3)
- n = 2 : 최근 두 달치만 보기 때문에 shock이 생기면 바로 그것을 반영함.
- n = 7 : 7달치를 보기 때문에 두 달치만 볼 때보다, shock을 늦게 따라감. (그대로 낮은/높은 수요값이 남겨져 반영)
- 즉, n값이 작을수록 최근 변화에 빠르게 반응한다.
- Exponential Smoothing(method 5); $\alpha$가 0.9, 0.2 일 때. 각각 비교해보자.
- $\alpha$ = 0.9 : 최근 달의 수요값을 90%로 많이 보기 때문에 shock이 생기면 바로 그것을 반영함.
- $\alpha$ = 0.2 : 최근 달의 수요값을 20&로, 이전 달의 수요값을 80%로 두었기 때문에 늦게 따라감.
- 즉, $\alpha$값이 높을수록 최근 변화에 빠르게 반응한다.
Example2 :
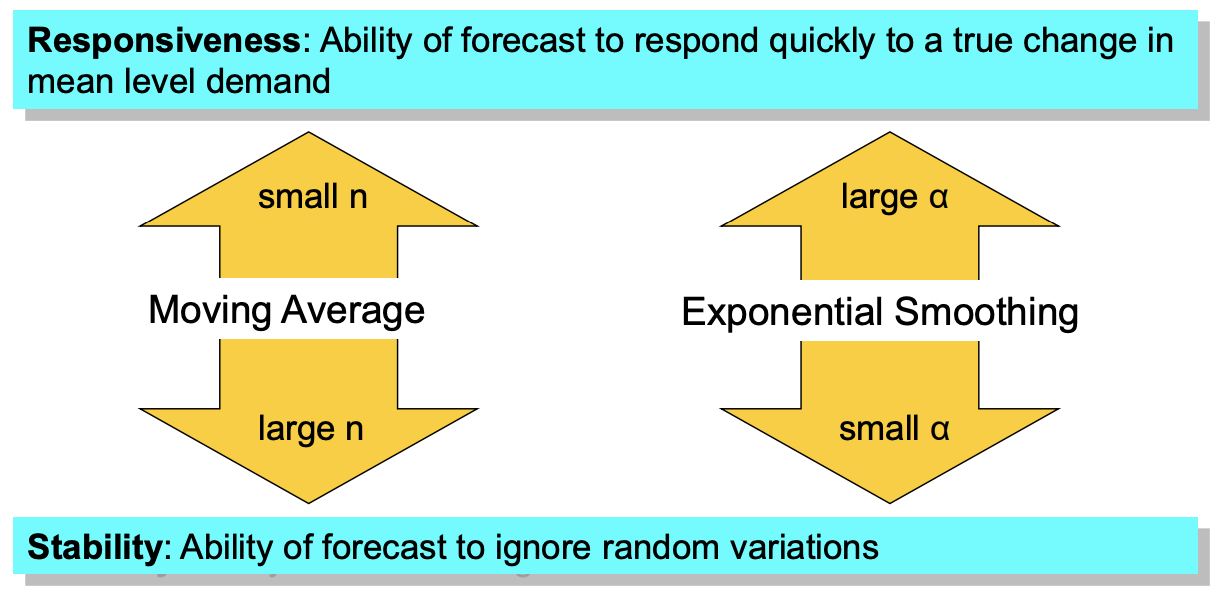
- stable이 중요한 경우.
- → 최근 변화에 빠르게 반응할수록 = responsibility가 클수록, 원래 수요로 돌아오기 어렵다.
Forecast Error
- $e_t$(Forecast Error) = $A_t$(Demand) - $F_t$(Forecast)
Mean Forecast Error (MFE)
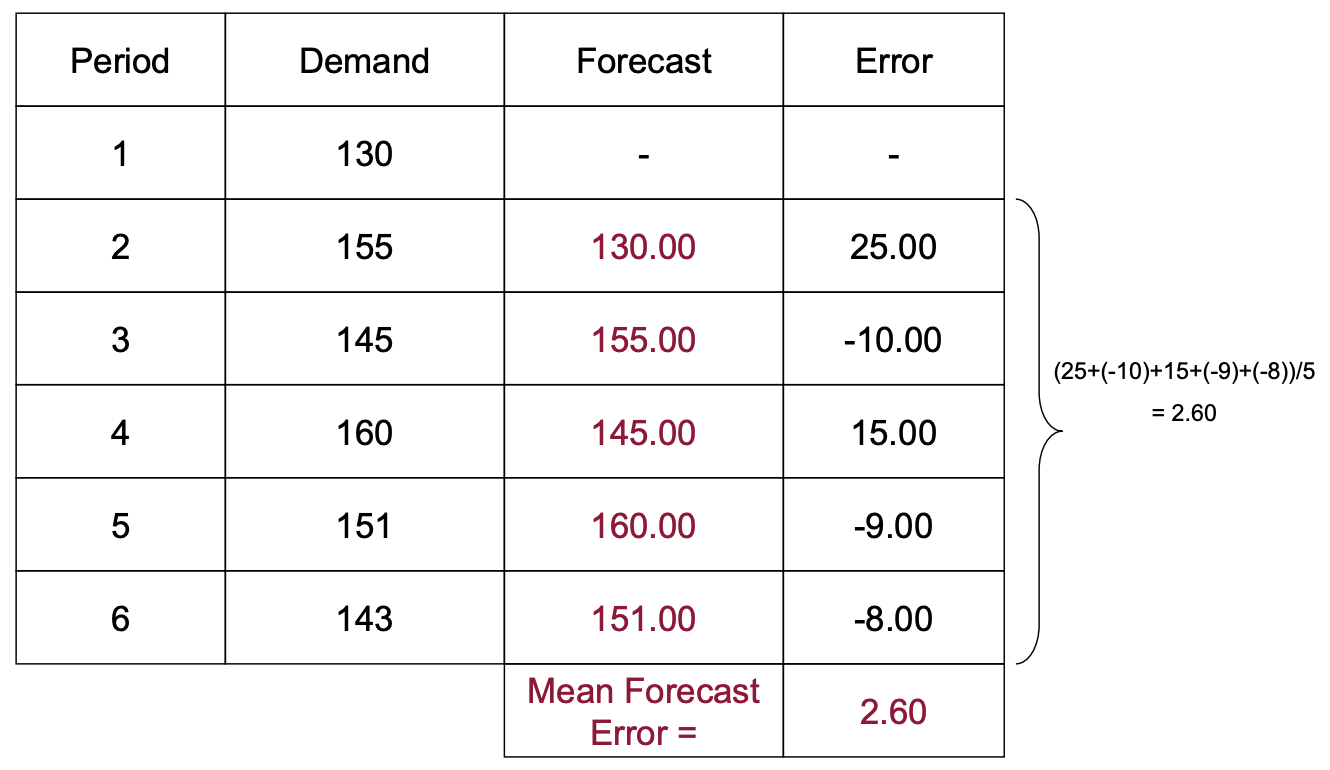
- 부호가 존재해서 에러에 대한 합을 구했을 때, 결국 0이 될수도 있음.
Mean Absolute Error (MAE)
- 에러에 대한 절대값을 취해서, 부호를 없애버림.
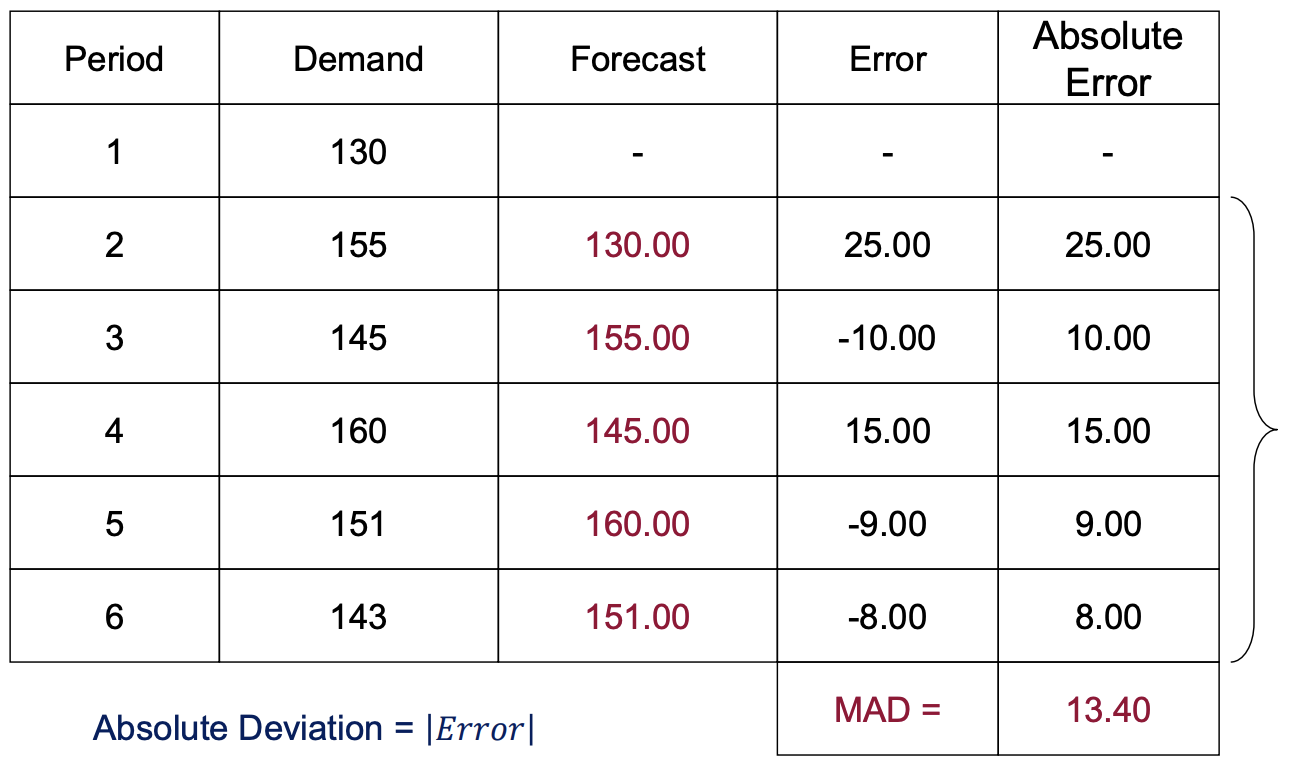
Mean Square Error (MSE)
- 에러에 제곱을 취해서, 부호를 없애버림.
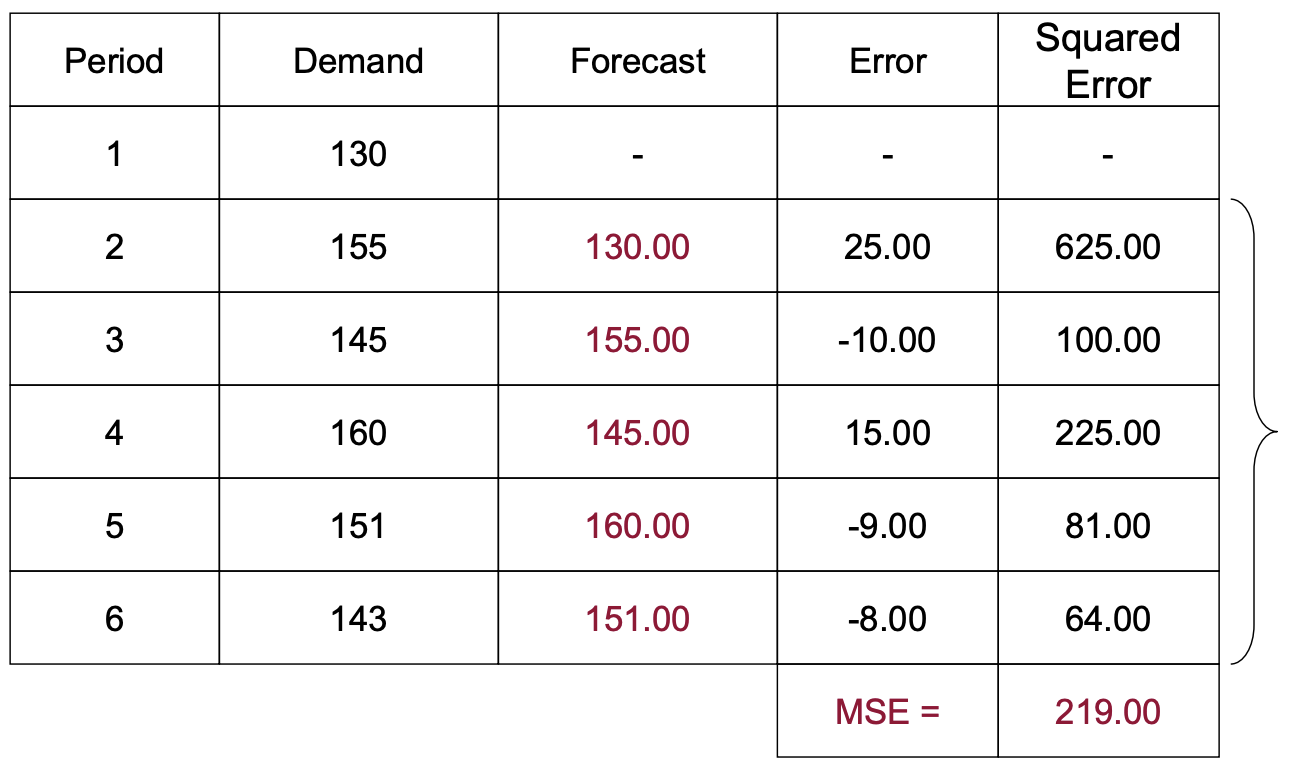
- 에러가 클수록, 제곱값이 훨씬 커져 큰 에러값이 더 커진다. (일종의 패널티)
- → 작은 에러는 수용하되, 큰 에러가 발생하는 것을 피하고 싶을 때 MAE보다 좋음.
Mean Absolute Percentage Error (MAPE)
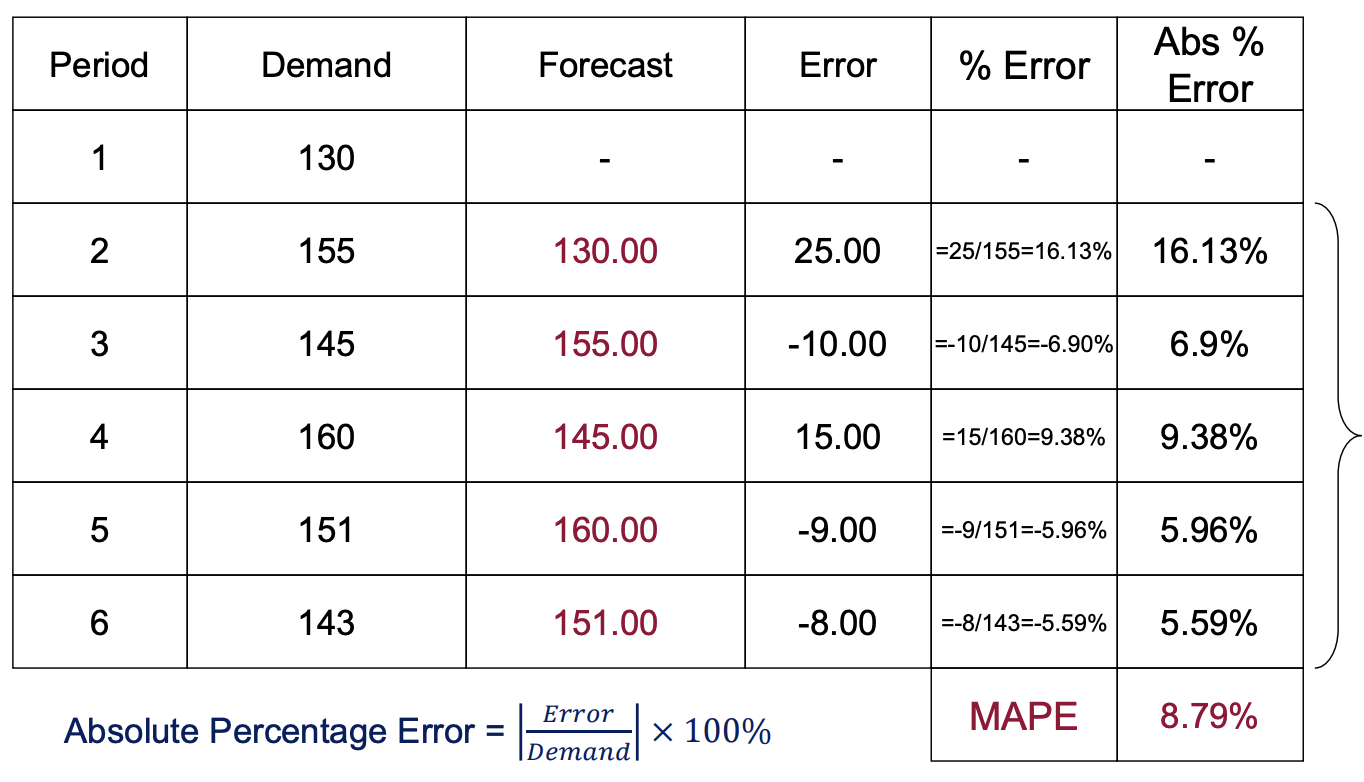
'* ML | DL > LG Aimers' 카테고리의 다른 글
| [LG Aimers] Forecasting (2) 트렌드와 계절성을 반영한 수요예측 (0) | 2023.07.23 |
|---|










