[트리] 이진 트리, 힙, 세그먼트 트리
2023. 7. 26. 12:54
트리 Tree
- 트리의 조건 : 1개 이상의 노드를 갖는 집합(그래프) + cycle이 없다.
- 노드 N, 간선 M
- cycle : 간선이 N−1 일 때, 사이클이 없다.
- cycle이 존재하지 않는다 = 우회도로가 없다 = 경로가 하나뿐이다.
이진 트리 Binary Tree
- 트리의 분지 수가 2 이하인 트리.
- 트리의 분지 수 : 트리 내의 모든 노드의 차식 차수 중 가장 큰값을 나타냄.
- => 즉, 자식을 최대 2개 가질 수 있다.
- 높이가 H일 때, 노드의 최대 개수는 2H−1이다.
힙 Heap
- 완전 이진트리 형태
- 힙 조건 (Heap condition) 만족
- max heap : 모든 노드들은 자식 노드보다 큰 값을 가진다. (루트노드가 가장 큰 값)
- min heap : 모든 노드들은 자식 노드보다 작은 값을 가진다. (루트노드가 가장 작은 값)
- 삽입과 삭제가 O(logN)
- 삽입과 삭제 연산이 빠르므로 정렬, 최대/최대 값을 찾을 때 사용한다.
- 삽입 : 가장 마지막 위치에 노드를 삽입하고, 힙 조건을 만족할 때까지/루트에 도달할 때까지 부모-자식 교체.
- 삭제 : 루트 노드를 삭제하고, 마지막 노드를 루트노드에 가져와, 힙 조건을 만족할 때까지/리프에 도달할 때까지 부모-자식 교체.
- 이는 최대 트리의 높이만큼 연산될 수 있다. 따라서 노드 N개의 트리 높이인 logN의 시간 복잡도를 가짐.
세그먼트 트리
https://www.acmicpc.net/blog/view/9

- 리프노드가 아닌 노드에 써진 숫자(internal) : 해당 노드가 커버할 수 있는 인덱스 수.
- 예시) 0
9 : 0에서 9까지 커버. 그 아래 자식인 04 / 5~9 는 각각 0에서 4까지, 5에서 9까지 커버.
- 예시) 0
- 리프노드(external) : 오직 하나의 값만 커버.
- 루트노드에 인덱스 범위를 지정해준다.
- 자식노드에 반씩 지정해준다.
- (시작, 끝) → (시작, (시작+끝)/2) / ((시작+끝)/2, 끝)
노드를 찾는 방법
- 자식에게 계속 물어봄.
- 자식이 만약 그 범위를 모두 포함하고 있으면, 전파하지 않고 바로 부모에게 알려줌.
- 자식이 만약 그 범위를 일부 포함하고 있으면, 아래로 전파.
예시1. 0~4 찾기 - 만약 자식에 해당 범위가 포함되지 않으면 그때부터 전파 X, false 리턴. (+합/곱 연산에 영향을 주지 않는 수 리턴)
예시2. 1
~ 5 찾기
1. 왼쪽 자식 (0\~
4), 오른쪽 자식 (5
9)
- 왼쪽 자식 : 불필요한 범위가 포함되어 있음. 다시 한 번 자식들에게 전파. -> 리턴
2. 왼쪽 자식 (0
2), 오른쪽 자식 (2~4)
- 왼쪽 자식 : 불필요한 범위가 포함되어 있음. 다시 한 번 자식들에게 전파. -> 계산 후, 리턴
3. 왼쪽 자식 (0), 오른쪽 자식 (1)
- 왼쪽 자식 : 자신의 값 0 올려줌. (하지만 포함은 X)
- 오른쪽 자식 : 자신의 값 1 올려줌. -> 부모에 이를 리턴함. 부모는 이를 계산.
- 오른쪽 자식
- 오른쪽 자식 :
탐색 횟수 (시간복잡도)
- 리프 노드의 개수는 가져야할 데이터의 개수와 똑같음. -> 데이터가 n개이면 n개의 리프 노드. 이를 갖는 트리의 높이는 2h>=data개수를 만족해야 함. 따라서 트리의 높이는 h=log2N
- 한번 루트에서 자식에게 가는 횟수는 logN 인데.
- 중간에서 끝나거나
- 리프노드까지 갈 수 있음. (근데 이 경우의 수는 생각보다 많지 않음.)
- => 따라서 logN으로 생각.
업데이트
원래 값과의 변경된 값과의 차이를 구함.
- 부모를 따라 내려가면서 (해당되는 범위이면) 차이를 더해줌.
- 리프 노드에 도달하면 끝.
logN의 시간복잡도.
-> 부분최대값, 부분합, 부분머시기 : 세그먼트 트리를 이용할 확률이 높음. (부분합이라고 모두 세그먼트트리는 아님...)
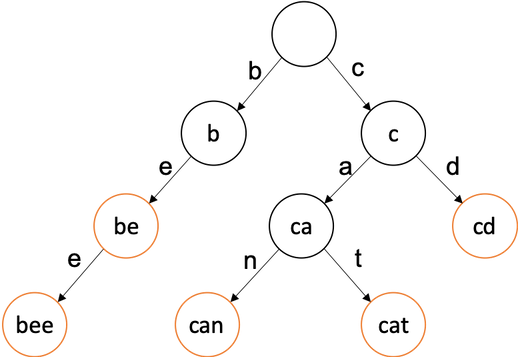
트라이 Trie
'* 언어 | 알고리즘 > 알고리즘 개념' 카테고리의 다른 글
| [트리] 최단경로 찾기 : 플로이드-워셜, 다익스트라, 벨만포드 (0) | 2023.08.03 |
|---|---|
| [트리] LCA, 오일러 투어, 단절점 찾기, (0) | 2023.08.01 |
| [그래프] 서로소 집합 Union-Find, 위상정렬, 최소신장트리 (0) | 2023.07.31 |
| [트리] 펜윅 트리 (0) | 2023.07.27 |
| [정수론] 합동식의 성질, 에라토스테네스의 체, (확장) 유클리드 호제법 (0) | 2023.07.27 |













